VĒL PROGRAMMU PIEMĒRI: Tipiski skolu programmēšanas 8 uzdevumi, pārnesti uz Scratch
Izpildes nosacījumi
+ Noderīgi 8 uzdevumi ievadam programmēšanā. Vairāk vai mazāk klasiski programmēsanas priekšmetu skolas uzdevumi, izpildāmi ne tikai Free Pascal, C++, Java, Visual Basic, bet arī Scratch: mērvienību kalkulators, varbūtību eksperiments, pirmskaitļi, Fibonači skaitļi, Lisažū figūras, fraktāļi un MS Excel funkcijai PMT() līdzīgi aprēķini.
Materiāla autors doc. Imants Gorbāns.
7. Fraktāļu koks
Fraktālis ir ģeometriska figūra, kura sastāv no vairākām (principā bezgalīgi daudzām) daļām, kas ir līdzīgas visai figūrai kopumā. Fraktāļus var iegūt, atkārtoti dalot kādu figūru vai virsmu aizvien sīkākās daļās, skat. http://lv.wikipedia.org/wiki/Frakt%C4%81lis.
Fraktāļi var būt dažādi, viens no to veidiem ir fraktāļu koks, tas ir interesants ar to, ka arī LU DF emblēmā ir fraktāļu koks. Aplūkosim vienu no fraktāli zīmējošas programmas versijām.
Koka zīmēšana aprakstāma šādos soļos:
a) aicinam lietotāju ievadīt sākotnējo (garāko) stubra garumu,
b) uzzīmējam stumbru,
c) uzzīmējam zaru pa labi,
d) uzzīmējam zaru pa kreisi,
e) katru no zariem uzskatam par nākamā, mazākā koka stubru (izmantojam rekursiju),
f) pārtraucam zīmēt, ka zari šķiet pārāk mazi.
Lai labāk saprastu šāda tipa uzdevumus, ir jāiepazīstas ar rekursijas jēdzinu, kas ir viens no svarīgākajiem programmēšanā. Par Scratch rekursijas iespējām ieteicams izlasīt http://wiki.scratch.mit.edu/wiki/Recursion.
Programma skaistuma pēc katra soļa maina krāsu, kā arī ir fona mūzika. Izpētiet programmas kodu, pamēģiniet saprast, kā tā darbojas, kas notiek, ja maina tajā ieslēptos skaitliskos parametrus.

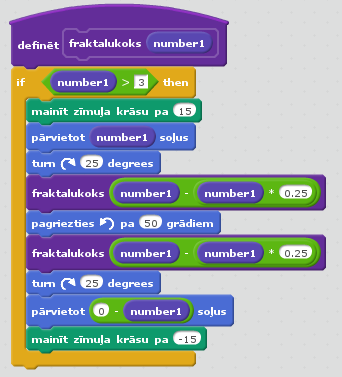
18. att. Fraktāļu koka programmas galvenā daļa.
Programmas URL: http://scratch.mit.edu/projects/26296814/ .
UZDEVUMI:
a) uzlabojiet programmu, lai fona mūzika beidzas līdz ar fraktāļa uzzīmēšanu,
b) atrodiet Scratch portālā dažādas fraktāļu programmas un papētiet,
c) pārveidojiet/ izveidojiet programmu tā, ka tiek izmantota pārvietošanās uz konkrētām koordinātām x un y, nevis iešana pa attālumu un pagriešanās kā šajā piemērā.
Fraktāļi var būt dažādi, viens no to veidiem ir fraktāļu koks, tas ir interesants ar to, ka arī LU DF emblēmā ir fraktāļu koks. Aplūkosim vienu no fraktāli zīmējošas programmas versijām.
Koka zīmēšana aprakstāma šādos soļos:
a) aicinam lietotāju ievadīt sākotnējo (garāko) stubra garumu,
b) uzzīmējam stumbru,
c) uzzīmējam zaru pa labi,
d) uzzīmējam zaru pa kreisi,
e) katru no zariem uzskatam par nākamā, mazākā koka stubru (izmantojam rekursiju),
f) pārtraucam zīmēt, ka zari šķiet pārāk mazi.
Lai labāk saprastu šāda tipa uzdevumus, ir jāiepazīstas ar rekursijas jēdzinu, kas ir viens no svarīgākajiem programmēšanā. Par Scratch rekursijas iespējām ieteicams izlasīt http://wiki.scratch.mit.edu/wiki/Recursion.
Programma skaistuma pēc katra soļa maina krāsu, kā arī ir fona mūzika. Izpētiet programmas kodu, pamēģiniet saprast, kā tā darbojas, kas notiek, ja maina tajā ieslēptos skaitliskos parametrus.

18. att. Fraktāļu koka programmas galvenā daļa.

19. att. Fraktāļu koka programmas apakšprogramma (izveidotā funkcija).

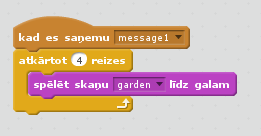
20. att. Fona mūzika (skatuves skripts).
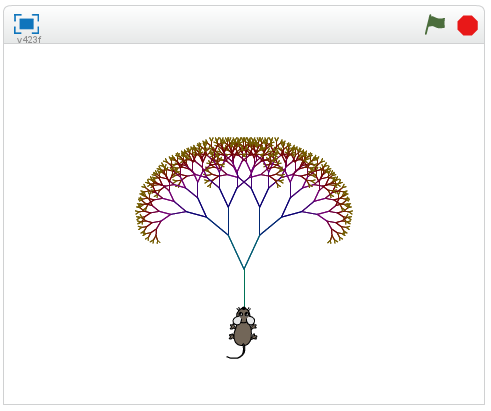
21. att. Fraktāļu koka programmas rezultāts pie ievaddatiem = 50.
Programmas URL: http://scratch.mit.edu/projects/26296814/ .
UZDEVUMI:
a) uzlabojiet programmu, lai fona mūzika beidzas līdz ar fraktāļa uzzīmēšanu,
b) atrodiet Scratch portālā dažādas fraktāļu programmas un papētiet,
c) pārveidojiet/ izveidojiet programmu tā, ka tiek izmantota pārvietošanās uz konkrētām koordinātām x un y, nevis iešana pa attālumu un pagriešanās kā šajā piemērā.