VĒL PROGRAMMU PIEMĒRI: Tipiski skolu programmēšanas 8 uzdevumi, pārnesti uz Scratch
| Vietne: | E-izglītība |
| Kurss: | Jauno datoriķu skola |
| Grāmata: | VĒL PROGRAMMU PIEMĒRI: Tipiski skolu programmēšanas 8 uzdevumi, pārnesti uz Scratch |
| Drukājis: | Vieslietotājs |
| Datums: | piektdiena, 2026. gada 30. janvāris, 19:11 |
Apraksts
+ Noderīgi 8 uzdevumi ievadam programmēšanā. Vairāk vai mazāk klasiski programmēsanas priekšmetu skolas uzdevumi, izpildāmi ne tikai Free Pascal, C++, Java, Visual Basic, bet arī Scratch: mērvienību kalkulators, varbūtību eksperiments, pirmskaitļi, Fibonači skaitļi, Lisažū figūras, fraktāļi un MS Excel funkcijai PMT() līdzīgi aprēķini.
Materiāla autors doc. Imants Gorbāns.
Ievads
Daži piemēri, varbūt kādam noder.
![]() Visi Latvijas Universitātes Datorikas fakultātes Jauno datoriķu skolas materiāli ir licencēti. Autors Imants Gorbāns šo materiālu ir licencējis ar Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported licenci.
Visi Latvijas Universitātes Datorikas fakultātes Jauno datoriķu skolas materiāli ir licencēti. Autors Imants Gorbāns šo materiālu ir licencējis ar Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported licenci.
1. Mērvienību pārrēķināšanas kalkulators
Aplūkosim tipisku uzdevumu, kas rodas autovadītājam Latvijā, kad tas nopircis lietotu auto no ASV. Problēma ir mērvienības dažādos paneļa rādījumos, piemēram, atālums tiek uzrādīts jūdzēs (miles), ātrums - jūdzēs stundā (mph - miles per hour), degvielas patēriņš - jūdzēs uz galonu. Lai saprastu, kas notiek, Eiropas cilvēkam vismaz sākumā ir šie skaitļi jāpārrēķina uz km, km/h, l/100km.
Aplūkosim ātruma pārveidošanu no mph uz km/h. Tā kā viena šajā sakkarā lietotā jūdze ir 1,609344 km, tad ir viegli ieraudzīt formulu: ātrums_LV = ātrums_US * 1,609344 (zvaigznīte * ir reizināšanas simbols programmēšanas valodās).
Programmu veidosim tā, ka katru reizi pēc atstarpes taustiņa nospiešanas var veikt jaunu aprēķinu, zaļo karodziņu atkārtoti nespiežot. Līdz ar to vienkāršākais šādas programmas koda variants dots 1. attēlā, tomēr tam ir vismaz viena būtiska nepilnība - rezultāts nav noapaļots.
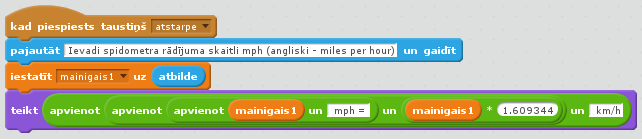
1. att. Scratch kods v.1 mph uz km/h.
Lai rezultātu noapaļotu līdz 2 cipariem aiz komata, ir jāizveido neliels algoritms, jo Scratch iebūvētā noapaļošana noapaļo veselos skaitļos. Algoritma ideja ir vienkārša: vispirms skaitli pareizinam ar 100, tad noapaļojam un tad izdalam ar 100. Skat. 2. att., tajā dalīšana (/) nav pievienota 'mainīgais2' izteiksmei, bet nākamajā rindā, lai parādītu, ka Scratch pieļauj aritmētiskās darbības arī operatorā teikt (say).
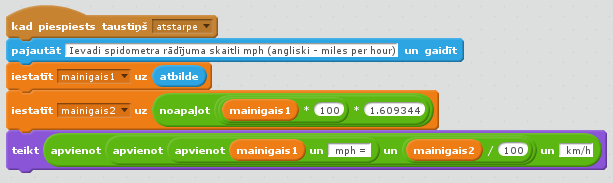
2. att. Scratch kods v.2 mph uz km/h.
Tā kā jebkuru programmu vienmēr var pilnveidot, tad pievienosim pārbaudi, vai lietotāja ievadītie dati vispār ir skaitlis. Ja to neizdara, Scratch atgriež rezultātu nulle, bet citas programmēšanas valodas nav tik saprotošas un tajās ievaddatu pārbaude ir ļoti vēlama. Kā viegli ieraudzīt, pārbaudes algoritms var būt vienkāršs: ja 'mainigais1'*1='mainigais1' , tad ievadīts ir skaitlis, citādi gariņš saka, ka nebija skaitlis; jo burtu virkni reizinot nekas nesanāks- Scratch iekšienē būs kļūdas ziņojums, un tas nebūs vienāds ar ievadīto burtu virkni. Skat. programmiņas gala versiju 3. un 4. att.
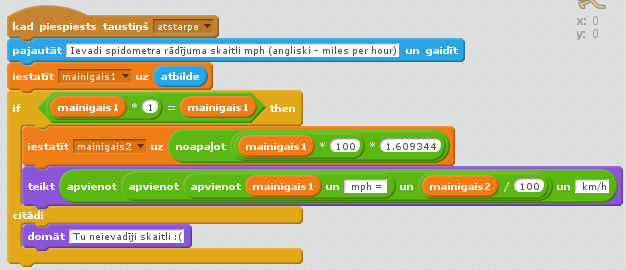
3. att. Scratch kods v.3 mph uz km/h.
4. att. Programmas saskarne.
Tā nu sanāca, ka šajā programmiņā tika pielietoti 2 mazi algoritmi, viens - noapaļošanai, otrs- ievaddatu pārbaudei.
Programmiņu var padarbināt tiešsaistē: http://scratch.mit.edu/projects/25680429/
UZDEVUMI:
1. Izveido programmu, kas rēķina pretēji - km/h uz mph.
2. Izveido programmu, kas rēķina degvielas patēriņu mpg uz l/100km, pārveidojumiem nepieciešamos datus var atrast tiešsaistes resursos (1 Mile per gallon = 235.214583 l/100km).
2. Varbūtība
Dzīvē nākas saskarties ar dažādiem varbūtiskiem procesiem, piemēram, metot spēļu kauliņu, metot monētu, spēlējot loteriju, izvēloties respondentus aptaujai, zināmā mērā arī veicot laika prognozi, šaujot mērķī, melojot utt. Tās ir situācijas, kurās precīzi rezultātu nevar paredzēt.
Aplūkosim monētas mešanu. Ideālai monētai varbūtība, ka tā nokritīs ar vinu pusi uz augšu ir 50% un arī ar otru pusi uz augšu - 50%. Tomēr šāds sadalījums (puse uz pusi) parādīsies tikai pie ļoti liela atkārtojumu skaita. Metot vienu vai dažas reizes, rezultāts nav prognozējams. Būtiski, ka arī pie miljons atkārtojumiem nākamā mēģinājuma konkrētais rezultāts ir tikpat neprognozējams kā pirmajā metienā. Bet mēs varam prognozēt situāciju kopumā: aptuveni pusmiljons metienos no miljona nokritīs ar vērtības skaitli uz augšu.
Ir zināmā mērā interesanti eksperimentāli pārbaudīt, pie cik liela atkārtojumu skaita rezultāts (biežums) ir 50% pret 50%, +/- 1. Izveidosim Scratch programmu, kas virtuāli veic monētas metienus. Varbūtība šeit ir attiecība 'sagaidāmo rezultātu skaits' / 'visu rezultātu skaits'. Domas pieraksts formulas veidā: p = m /n. Ja vēlamies izteikt %, tad vēl viss jāpareizina ar 100.
Programma jautās, cik reizes atkārtot un tad ar cikla un nejaušas izvēles operatoru palīdzību skaitliski (ne vizuāli) simulēs monētas mešanu. Savā ziņā šāda programma palīdz novērtēt, no cik lieliem skaitļiem rezultāts top varbūtiski prognozējams, kā arī testē Scratch iebūvētās nejaušību funkcijas kvalitāti. Ievadot lielus skaitļus, piemēram, 5 vai 6 ciparu, nāksies mazliet uzgaidīt, kamēr programma izpildās uz dotās veikt spējas datora.
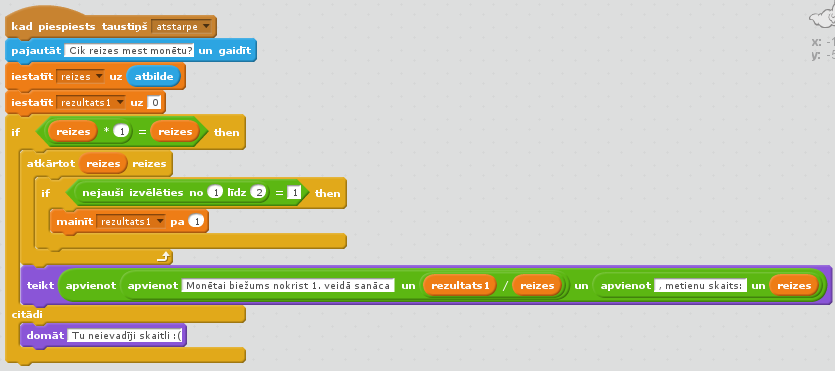
3. att. Varbūtību programmiņas kods.
4. att. Varbūtību programmiņas saskarnes izskats, atgiežot iegūto biežumu jeb "eksperimentālo varbūtību".
Programma tiešsaistē: http://scratch.mit.edu/projects/25684049/
UZDEVUMI:
1. Izveidojiet programmu, kas atgriež spēļu metamā kauliņa (1-6) rezultātu varbūtības.
2. Kā būs, ja metīsim reizē 2 vai 3 6-skaldņu kauliņus?
3. Skaitļa reizinātāji un pirmskaitlis
Nākamais klasiskais programmēšanas uzdevums ir skaitļa sadalīšana reizinātājos un noteikšana, vai tas nav pirmskaitlis. Ar reizinātāju sapratīsim skaitli, ar kuru var dalīt doto skaitli bez atlikuma.Programma ir mazliet garāka, tādēļ aplūkosim tās algoritma ideju vārdiskā aprakstā:
- Jāuzdod jautājums veikt skaitļa ievadi,
- jāpārbauda, vai ievadītie dati ir skaitlis (ja ievada ne-skaitli, piemēram, burtus, par to programma paziņo un reizinātājus nemeklē,
- ievadītais skaitlis tiek piešķirts kādam mainīgajam,
- pirms katra jauna skaitļa pārbaudes reizinātāju mainīgais jāiestata uz 1,
- reizinātāju skaita mainīgais jāiestata uz 2 (tas ir mazākais reizinātāju skaits - 1 un pats skaitlis),
- cikla atkārtojumu skaita mainīgais jāiestata uz 1,
- Scratch nav finkcijas MOD, tāpēc te nevar lietot pieeju "If number mod counter = 0, Then Set factors to Join (factors, counter, space), End If"; tā vietā vienkārši izdarīsim to pašu savādāk: "ja skaitlis, dalīts ar cikla numuru, ir vienāds ar skaitli, dalītu ar cikla numuru, kas noapaļots veselos skaitļos, tad ir atrasts reizinātājs",
- tad palielinām skaitītāju par 1 un izvadam reizinātāju.
- Ja reizinātāji ir tikai 1 un pats skaitlis (reizinātāju skaits ir 2), tad tas ir pirmskaitlis.
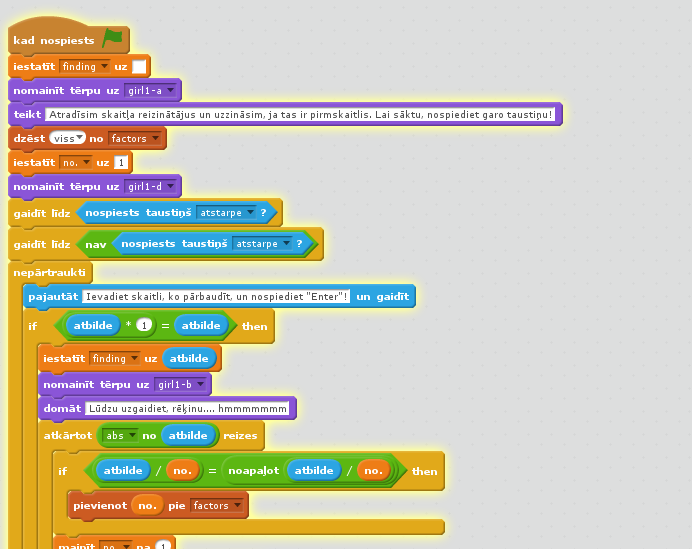
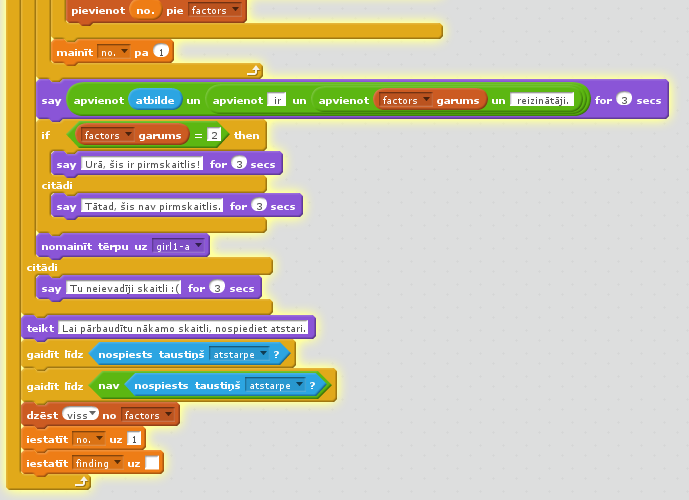
Programmu tiešsaistē var padarbināt un papētīt: http://scratch.mit.edu/projects/25716194/
UZDEVUMI:
1. Nomainiet gariņu uz citu tādu, kam ir vairāki tērpi, nokopējiet kodu uz jauno gariņu, meiteni izdzēsiet un veiciet programmā atbilstošas izmaiņas.
2. Izveidojiet programmu, kas atrod ievadīto skaitļu vidējo vērtību.
3. Izveidojiet programmu, kas atrod lielāko un mazāko no vairākiem ievadītajiem skaitļiem.
4. Fibonači skaitļi
Matemātikā par Fibonači skaitļiem sauc šādas virknes elementus: tās pirmie divi locekļi ir vienādi ar 1, bet katru nākamo locekli iegūst saskaitot divus iepriekšējos. Dažreiz par pirmajiem diviem virknes elementiem izvēlas skaitļus 0 un 1.
Programmiņas kods dots 8. att. un izskats 9. att.
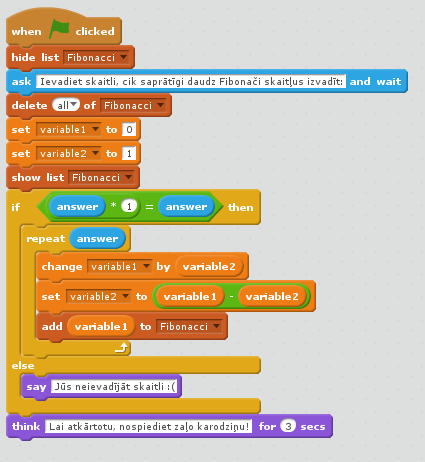
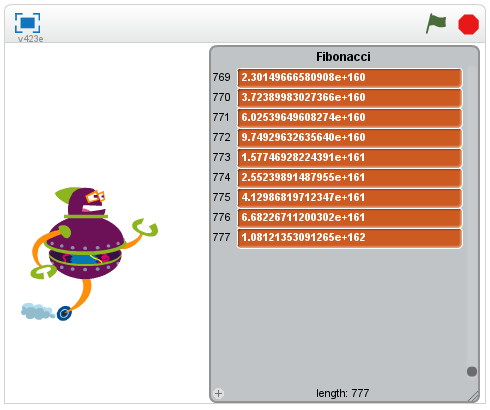
8. att. Fibonači skaitļu ģenerēšanas programmiņa no 1 un 1).
9. att. Fibonači programmiņas izskats.
Programmu var padarbināt tiešsaistē: http://scratch.mit.edu/projects/25718845/
Starp citu, cilvēka pirkstu kaulu un to delnas daļas garumi ir aptuveni tuvi Fibonači skaitļiem: 2; 3; 5; 8 (nags ir viena vienība). Precīzāk šajā sakarā gan var interesēties par "zelta griezumu".
UZDEVUMI:
1. Pārveidojiet programmiņu uz variantu, kad pirmie divi skaitļi ir 0 un 1.
2. Papildiniet programmu ar lūgumu uzgaidīt, ja aprēķins ieilgst.
5. Fibonači spirāle
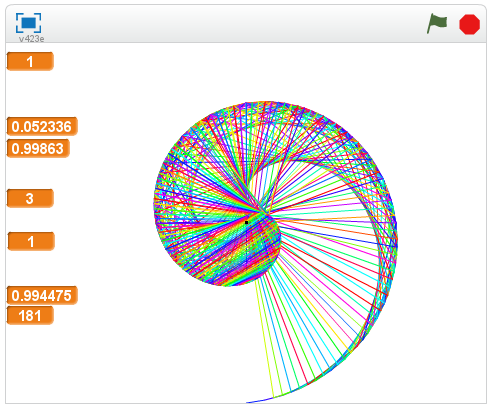
Fibonači taisnstūri var izveidot no atsevišķiem kvadrātiem, kuru malu garumi atbilst secīgiem Fibonači skaitļiem. Ja katrā no kvadrātiem ievelk 1/4 no riņķa līnijas, kuras rādiuss sakrīt ar kvadrāta malas garumu un kuras centrs atrodas attiecīgā kvadrāta virsotnē, iegūst Fibonači spirāli (tai ir zināma līdzību ar dažām gliemežnīcām). Skat. 10., 11. att.
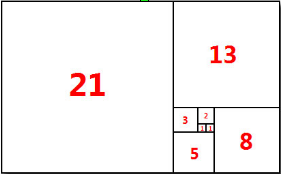
10. att. Fibonači kvadrāti.
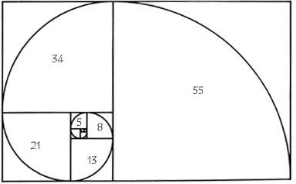
11. att. Fibonači spirāle.
Kā jau tika teikts pie iepriekšējā uzdevuma, Fibonači skaitļi katrs nākamais ir iepriekšējo 2 summa. Aplūkosim variantu, kas sākas ar 0 un 1: 0, 1, 1, 2 , 3, 5, 8, 13, 21, 34 ...... (0 + 1 = 1, 1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5 utt.).
Ja jūs pievienojat līnijas garumu no punkta uz ārējās spirāles malas līdz centram (0,0) citas līnijas garumam, kas iet tajā pašā virzienā no 0,0 līdz tuvākajam spirāle malas punktam, tad summa ir vienāda ar līnijas garumu, kas iet no pēdējā minētā punkta uz tālāko ārējo malu tādā pašā virzienā. Būtībā tas ir tas pats Fibonači skaitļu pieaugums, tikai izteikts ar garumiem. Izveidosim programmu, kas zīmē Fibonači spirāli. Programmai ir 3 gariņi (zīmēti punkti).
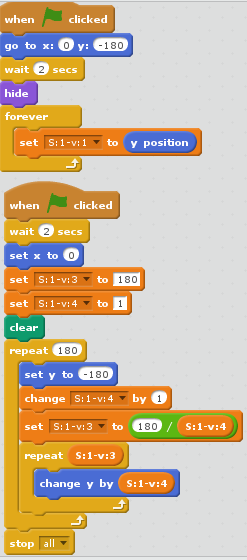
12. att. Gariņa S:1 kods.
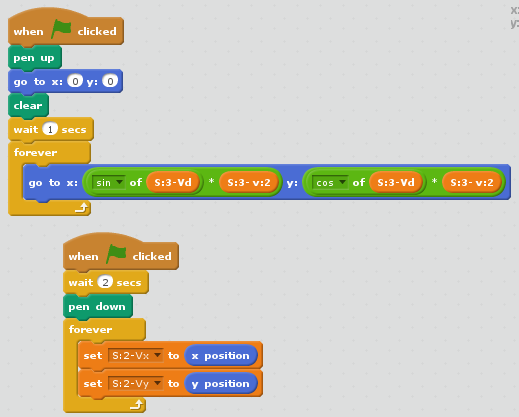
13. att. Gariņa S:2 kods.
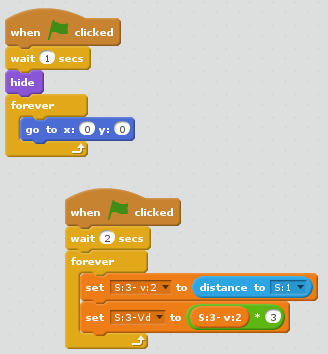
14. att. Gariņa S:3 kods.
15. att. Fibonači spirāles programmas rezultāts.
Programma tiešsaistē: http://scratch.mit.edu/projects/25719892/
UZDEVUMS:
1. Izveidojiet programmu, kas redzamu uzzimē tikai vienu, pašas Fibonači spirēles līniju.
6. Lisažū figurās
Lisažū figūras (Lissajous figure, curve) var viegli demonstrēt fizikas laboratorijā uz oscilogrāfa ekrāna, tās apraksta harmoniskas kustības. Šīs figūras matemātiski apraksta ar diviem parametriskiem vienādojumiem, kuru pamats ir: sin() funkcija:
x = A * sin(a*t+d) , y = B * sin(b*t)
Pirms pārdesmit gadiem Lisažū figūras bija gaismas noformējuma pamatideja lāzerdiskotēkās (ņem lāzeru ar līdz 5 mW jaudu un divus skaļruņus, pie kuru mebrānām pielīmēts neliels spogulītis; uz skaļruņiem laiž sinusoidālu spriegumu no skaņu ģeneratora; sistēmu izveido tā, ka lāzera stars vispirms krīt uz vienu spoguli, tad uz otru; spoguļu radītās stara novirzes ir savstarpēji perpendikulāras).
Izveidosim Scratch programmiņu, kas uz datora ekrāna zīmē Lisažū figuras līdzīgi kā tās var novērot uz oscilogrāfa ekrāna vai lāzerdiskotēkā. Programmiņas ideja ir:
1) notīram ekrānu un mainīgo t pēc iepriekšējās palaišanas,
2) novietojam zīmuli ekrāna centrā un to virtuāli piespīežam darbvirsmai,
3) veidojam ciklu, kas darbosies līdz pārtraukšanai (sarkanā poga),
4) cikla iekšienē pasakam, par kādu soli mainīsies mainīgais t,
5) ievietojam koda bloku "iet uz x: y:" un tajā ierakstam Lisažū figūras aprakstošās formulas, mainīgos a un b ļaujam lietotājam uz ekrāna mainīt ar bīdīšanu.
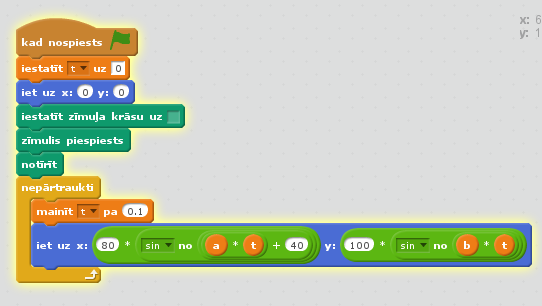
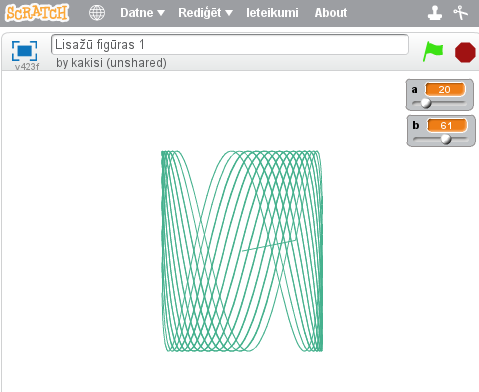
16. att. Lisažū figūru programa idejiski tīrā variantā
17. att. Viens no programmas zīmējumu rezultātiem.
Lai iegūtu savādākas figūras, maniet parametrus a un b, kā arī varat mainīt skaitliskos koeficientus programmas kodā.
Programmiņas URL adrese: http://scratch.mit.edu/projects/26291425/
UZDEVUMI:
a) uzzīmējeit figūras, kurām a un b attiecība ir kā 1:1, 1:2, 3:2, 3:4, 4:5.
b) izvidojiet programmu, kura prasa ievadīt a, b, c, d un zīmē līnijas pēc šādiem noteikumiem:
R = cos(m*t)+p
kur m=a/b un p=c/d
x(t) = R * cos (t)
y(t) = R * sin (t)
7. Fraktāļu koks
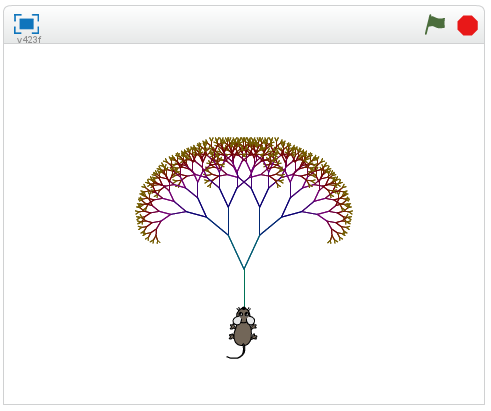
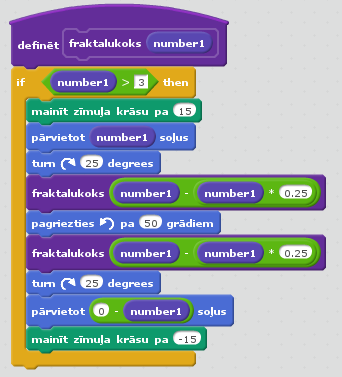
Fraktālis ir ģeometriska figūra, kura sastāv no vairākām (principā bezgalīgi daudzām) daļām, kas ir līdzīgas visai figūrai kopumā. Fraktāļus var iegūt, atkārtoti dalot kādu figūru vai virsmu aizvien sīkākās daļās, skat. http://lv.wikipedia.org/wiki/Frakt%C4%81lis.Fraktāļi var būt dažādi, viens no to veidiem ir fraktāļu koks, tas ir interesants ar to, ka arī LU DF emblēmā ir fraktāļu koks. Aplūkosim vienu no fraktāli zīmējošas programmas versijām.
Koka zīmēšana aprakstāma šādos soļos:
a) aicinam lietotāju ievadīt sākotnējo (garāko) stubra garumu,
b) uzzīmējam stumbru,
c) uzzīmējam zaru pa labi,
d) uzzīmējam zaru pa kreisi,
e) katru no zariem uzskatam par nākamā, mazākā koka stubru (izmantojam rekursiju),
f) pārtraucam zīmēt, ka zari šķiet pārāk mazi.
Lai labāk saprastu šāda tipa uzdevumus, ir jāiepazīstas ar rekursijas jēdzinu, kas ir viens no svarīgākajiem programmēšanā. Par Scratch rekursijas iespējām ieteicams izlasīt http://wiki.scratch.mit.edu/wiki/Recursion.
Programma skaistuma pēc katra soļa maina krāsu, kā arī ir fona mūzika. Izpētiet programmas kodu, pamēģiniet saprast, kā tā darbojas, kas notiek, ja maina tajā ieslēptos skaitliskos parametrus.

18. att. Fraktāļu koka programmas galvenā daļa.
Programmas URL: http://scratch.mit.edu/projects/26296814/ .
UZDEVUMI:
a) uzlabojiet programmu, lai fona mūzika beidzas līdz ar fraktāļa uzzīmēšanu,
b) atrodiet Scratch portālā dažādas fraktāļu programmas un papētiet,
c) pārveidojiet/ izveidojiet programmu tā, ka tiek izmantota pārvietošanās uz konkrētām koordinātām x un y, nevis iešana pa attālumu un pagriešanās kā šajā piemērā.
8. Kredīta aprēķins jeb PMT()
Izveidosim Scratch šaurā lokā plaši pazīstamo Excel funkciju PMT().
Tas ir aizņēmumu, kredītu aprēķinu uzdevums, kas ļauj labāk saprast summas un palīdz atbildīgi izlemt aizņemties vai nē. Uzdevums no reālās dzīves varētu būt šāds: "Preces cena ir 2000,00 €, prasītā sākuma iemaksa ir 0%, gada procentu likme 12%. Aprēķināt situācijas parametrus, ņemot kredītu uz 3 gadiem”. Tad tipiski dotās vērtības ievada Microsoft Excel vai OpenOffice.org Calc tabulā, lietojot funkciju PMT(). Aizdevuma summa = Cena * (1 - sākuma iemaksa %). Ja maksājuma periods ir 1 mēnesis, tad ikmēneša maksājuma summu rādīs finanšu funkcija PMT(Rate; NPer; PV; FV; Type) jeb PMT(procentu likme; maksājumu skaits; aizdevuma summa): Perioda iemaksa =PMT(gada procentu likme / 12; gadu skaits * 12; - Aizdevuma summa; gala summa; maksājuma tips), te pēdējos divus argumentus var nenorādīt, jo tie tipiski ir 0 (gala summa ir nulle un atmaksu veic katra mēneša sākumā nevis beigās). Pēc tam ir viegli aprēķināt kopējo samaksāto summu un bankas komisiju jeb ieņēmumu. Šādi viegli var papētīt rezultāta atkarību no procentu likmes un termiņa. PMT() funkcijs izpildījuma piemērs Excel alternatīvā OO.o Calc dots 22. att.
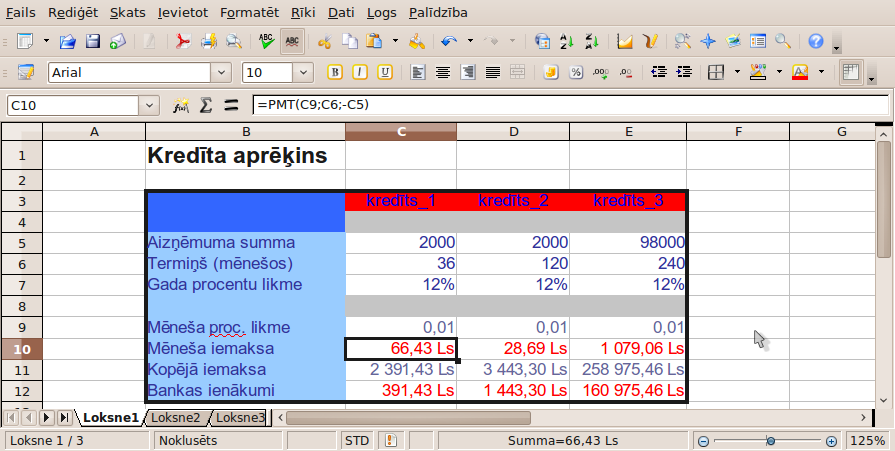
22. att. MS Excel funkcijas PMT() piemērs, izpildīts OpenOffice.org Calc.
Mēs esam pieraduši finanšu aprēķinus veikt Microsoft Excel vai alternatīvās, līdzīgās programmās. Bet kā būtu, ja šo programmu nebūtu, vai tās nebūtu mums pieejamas. Tad atbilstošo aprēķinu varētu uzprogrammēt. Piemēram, plaši pazīstamajā tīmekļa lapu veidošanas servera puses valodā PHP šis kods aizdevumam bez pirmās iemaksas būtu šāds, tikai jāuzmanās, lai viss ir 1 mēnesim: periodsgados*12, gadaprocenti/12:
<?php
$iprocenti = 12/12/100;
// Jo jāpāriet uz mēnešiem no gada un koeficienta formu no %.
$nilgums = 3*12;
$psumma = 2000;
function PMT($i, $n, $p)
{ return $i * $p / (1 - pow((1 + $i), -$n));
}
echo "Mēnesī jāatmaksā: ".(number_format(PMT($iprocenti, $nilgums, $psumma),2));
?>
Šis jaunas funkcijas definēšanas un izmantošanas PHP kods ir gandrīz pašsaprotams, tikai jāpaskaidro, ka pow() ir eksponentes funkcija PHP, kur pirmais mainīgais ir bāze, bet otrais- pakāpe.
Rēķinot ar kalkulatoru, mēnesī atdodamā summa, ko arī atgriež funkcija PMT(), būs:
= 12/1200 * 2000 / (1 - (1+12/1200)^(-3*12)). Mjā, kaut kā pagari, lai bankā sarunas karstumā ar šo nenokļūdītos- cik labi, ka mums ir Excel vai cita programma, kas māk to ātri sarēķināt!
Nelielu problēmu, aprēķinu programmējot Scratch rada tas, ka Scratch tieši nav pakāpes funkcijas, skat. http://wiki.scratch.mit.edu/wiki/%28%29_of_%28%29_%28Operators_block%29. No situācijias var iziet 2 veidos: a) izmantojot logaritmu ( y^x = 10^(x*lg(y)) ) vai b) vienkārši veidojot ciklu ar reizināšanu iekšā, skat. http://wiki.scratch.mit.edu/wiki/Solving_Exponents.
Ja veido ciklu, lai ietaupītu jūsu laiku eksperimentiem, pateikšu, ka Scratch nemāk izpildīt a=a*a, kaut māk a=a+1. Līdz ar to b variantā ciklā jāveido 1-2 pagaidu mainīgie starpvērtībām. Vēl jāpiebilst, ka Scratch nevar darboties ar ļoti lieliem skaitļiem, kas pie katra datora resursiem var atšķirties, jo programma pildās lokāli Flash spraudnī. Tādēļ tiek veikta rezultāta pārbaude: ja mainīgais, pereizināts ar, piemēram, 10, nemainās, tā saturs ir bezgalība vai 0, vai ir kļūdas paziņojums. Tad šajā gadījumā atgriešam speciālu atbildi, aicinot ievadīt mazākus skaitļus.
UZMANĪBU: nelietojiet programmu lieliem reāliem kredītu aprēķiniem, jo Scratch limitu dēļ tā pareizi strādā tikai ne visai lieliem skaitļiem! Bet nelielus kredītus ar šo sarēķināt var.
Kā iepriekšējās tēmās aplūkojām, Scratch noapaļošanas funkcija strādā tikai veselos skaitļos, tādēļ izmantojam iepriekš algoritmu: reizinam ar 100, tad noapaļojam, tad dalam ar 100 un tiek iegūts rezultāts ar 2 cipariem aiz komata.
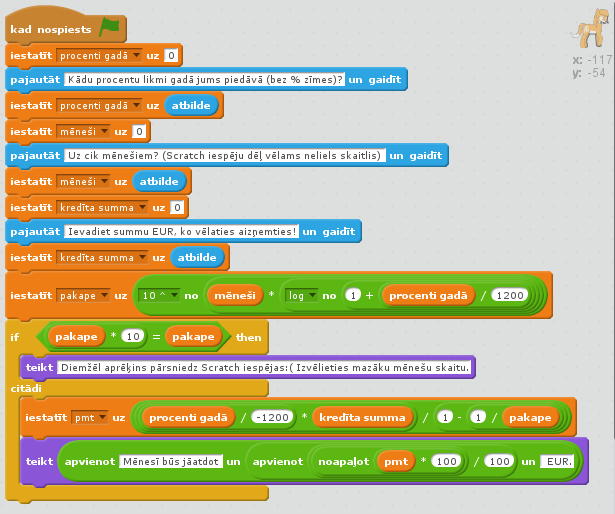
23. att. PMT programmas kods, tajā pakāpes funkcijas problēma atrisināta a veidā.
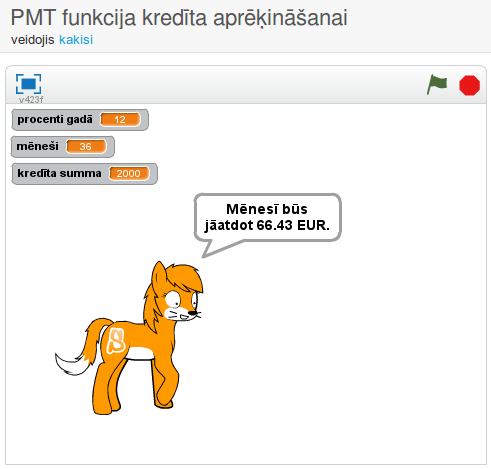
24. att. Programma darbībā.
Programmas adrese: http://scratch.mit.edu/projects/26351807/ .
UZDEVUMI:
a) papildiniet programmu, lai tā parāda, kāda ir kopējā atmaksājamā summa un cik notās ir komisija jeb aizdevēja kopējie ieņēmumi;
b) papildiniet programmu ar iespēju norādīt 1. iemaksas % vai summu;
c) izpētiet, šeit izmantotā PMT() formula atbilst kredīta atmaksai mēneša sākumā vai beigās, modificējiet formulu otram variantam (finansu funkciju formulas internetā var atrast, diemžēl dažos resursos tās ir kļūdainas);
d) izveidojiet analogu programu uzkrājumu veidošanas aprēķinu Microsoft Excel funkcijai FV(), skat. http://www.frickcpa.com/tvom/TVOM_formulas.asp.