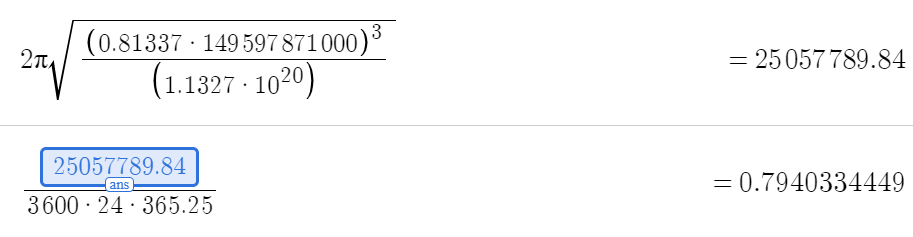Labdien!
Jautājumā 38 ir jāatrod asteroīda Saules apriņķošanas periods gados. No III. Keplera likuma
T = 2 pi sqrt(a^3/GM) un, izsakot sekundēs, pēc tam pārveidojot gados iznāk:
T = 0,7940 y
Oficiālā atrisinājumā piedāvātā pieeja pat no dimensionāliem apsvērumiem, šķiet, nekorekta.
Ar cieņu, Iļja Niks Stoligvo.